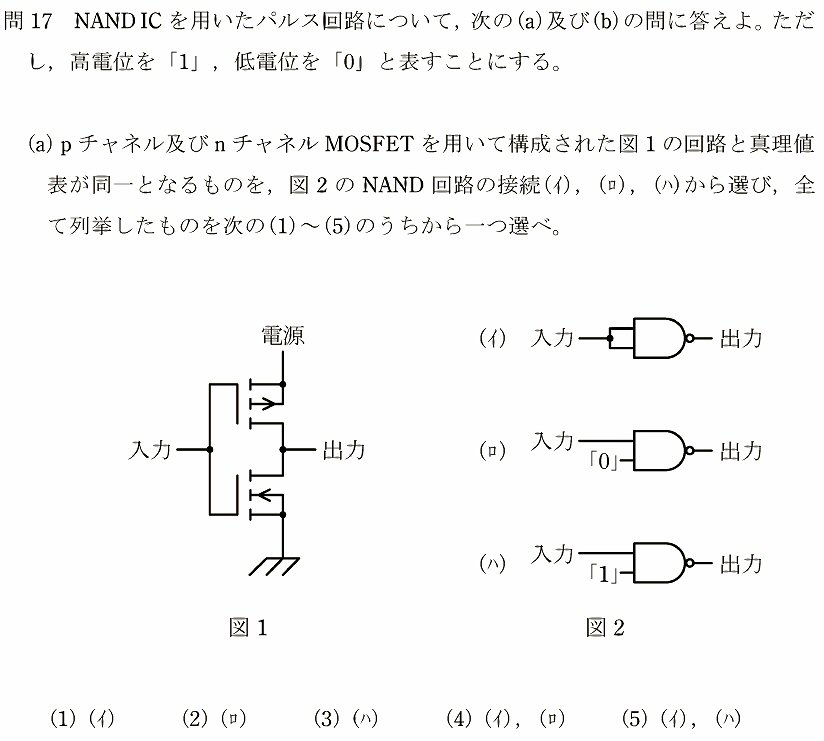
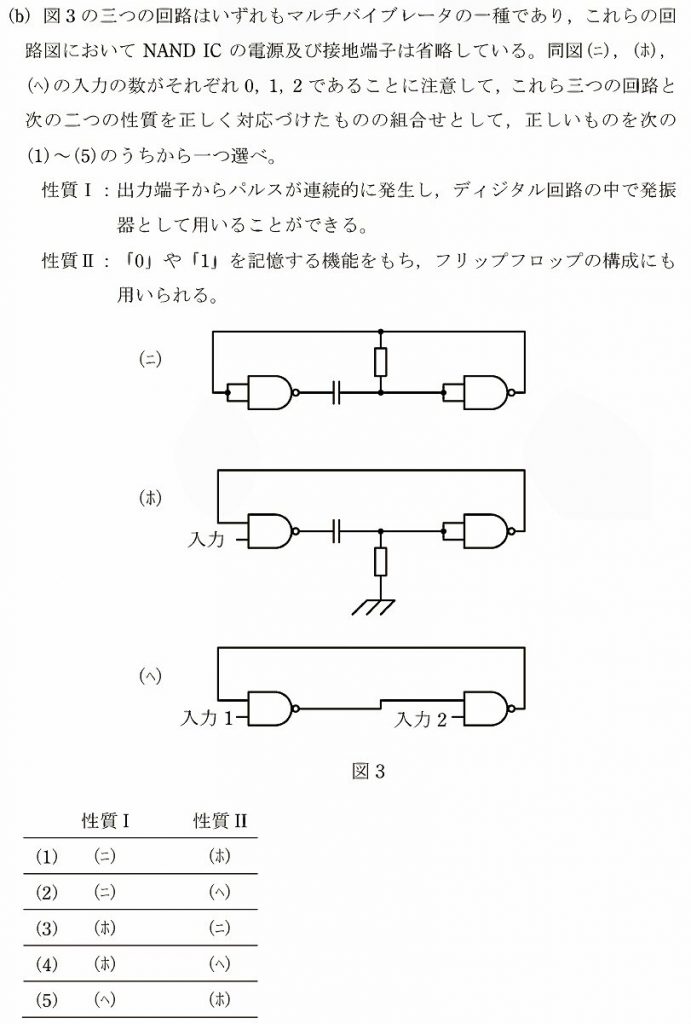
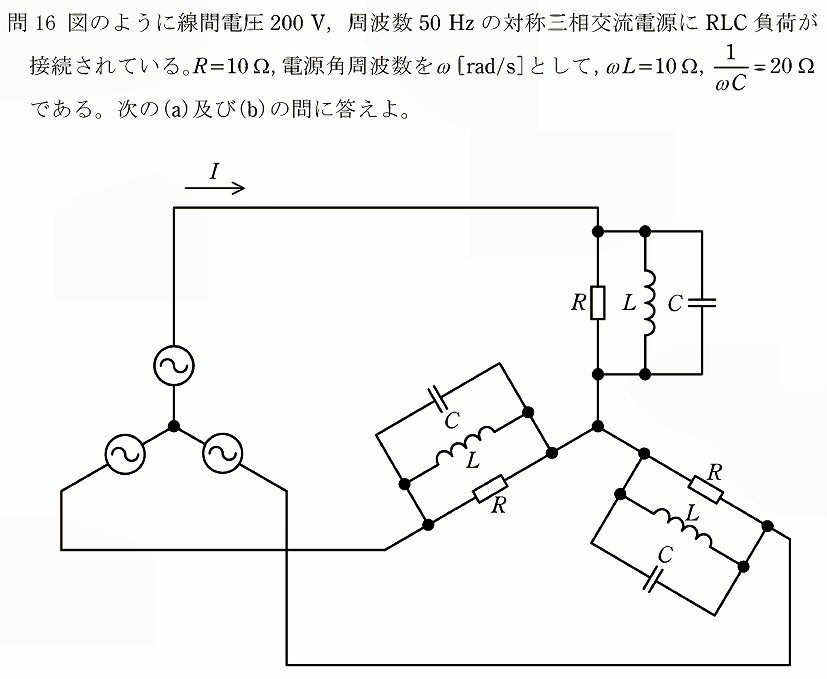
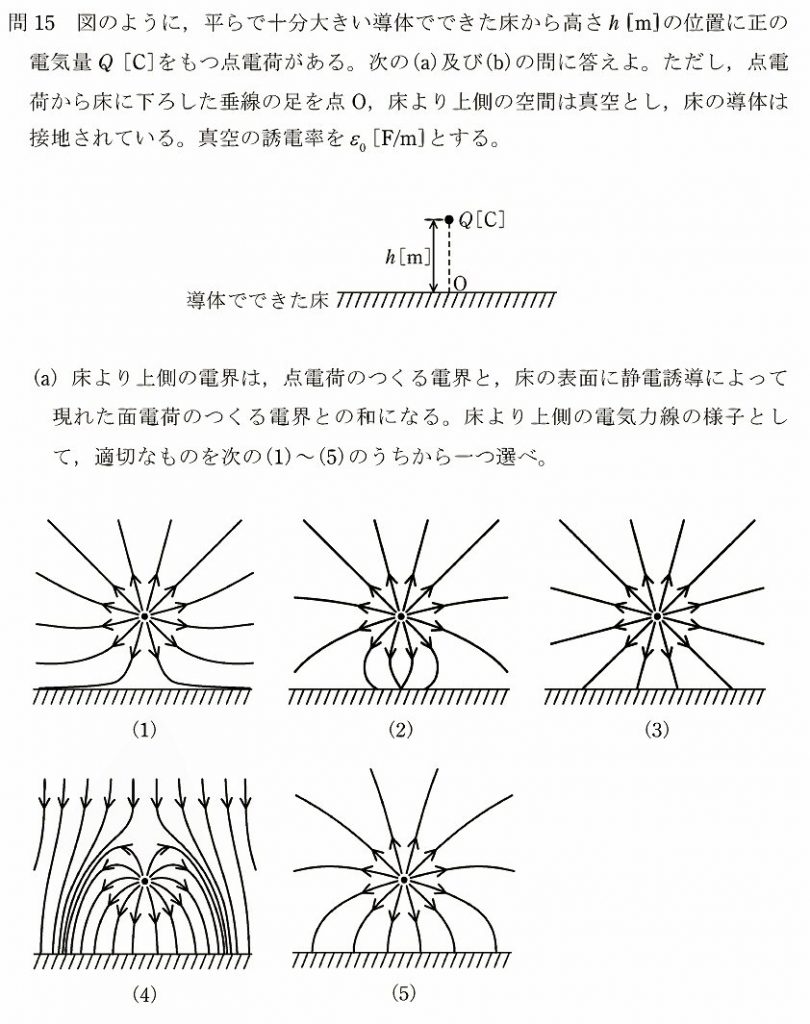
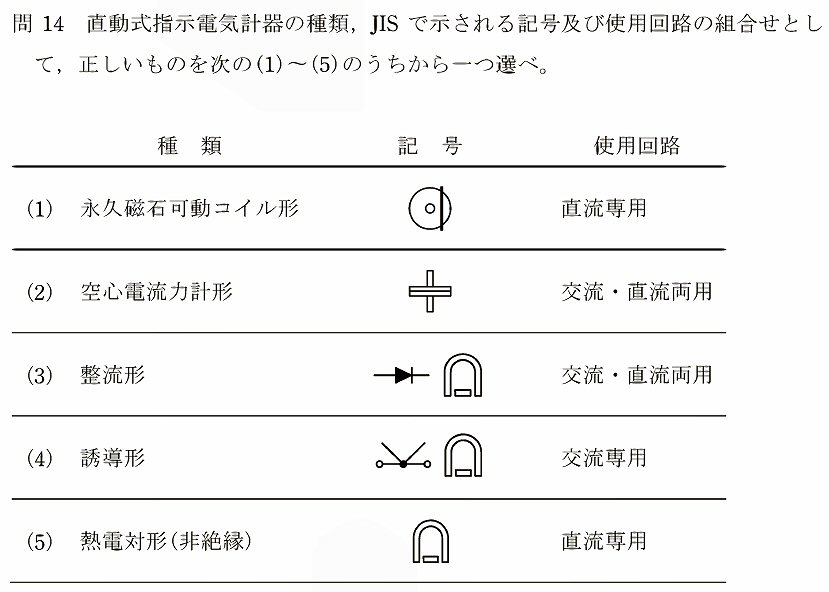
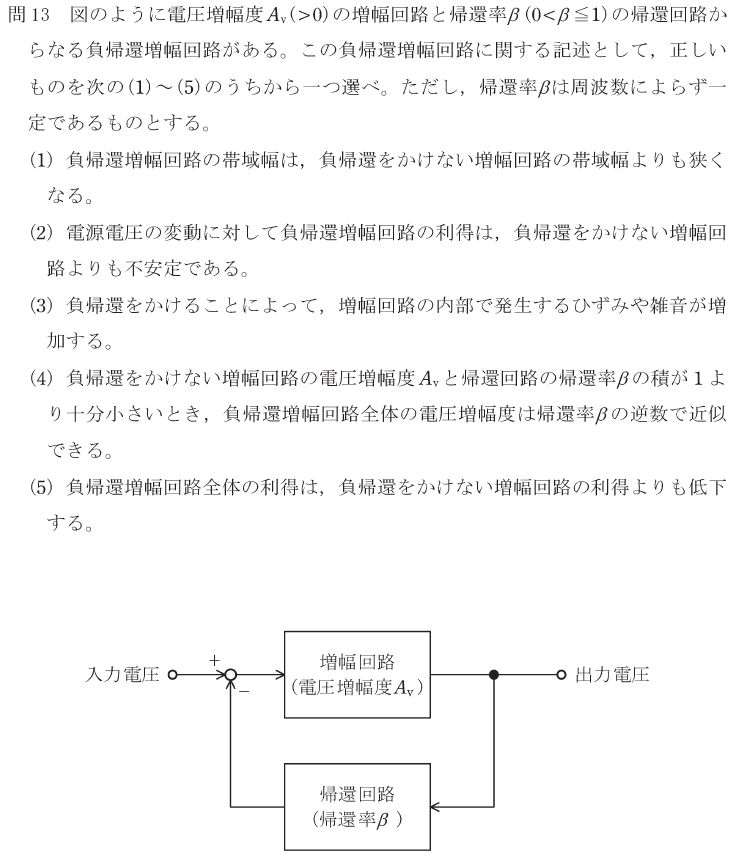
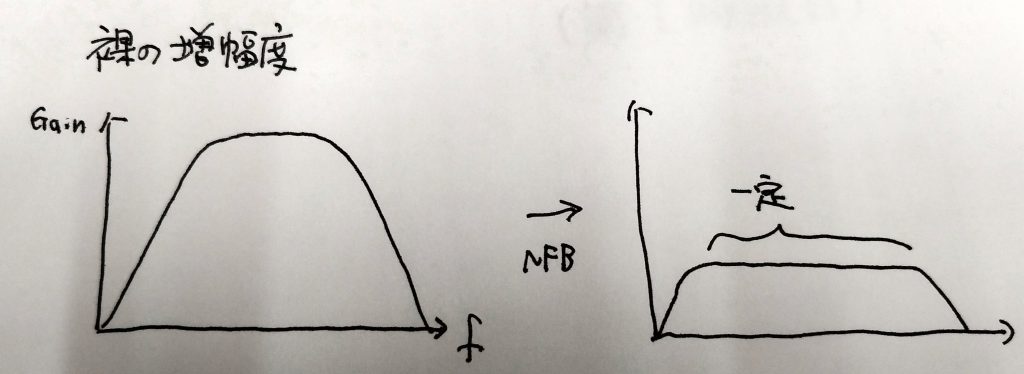
デジタルテスタ等で幅広く使われている二重積分型AD変換の基本原理に関する問題です。
(a)
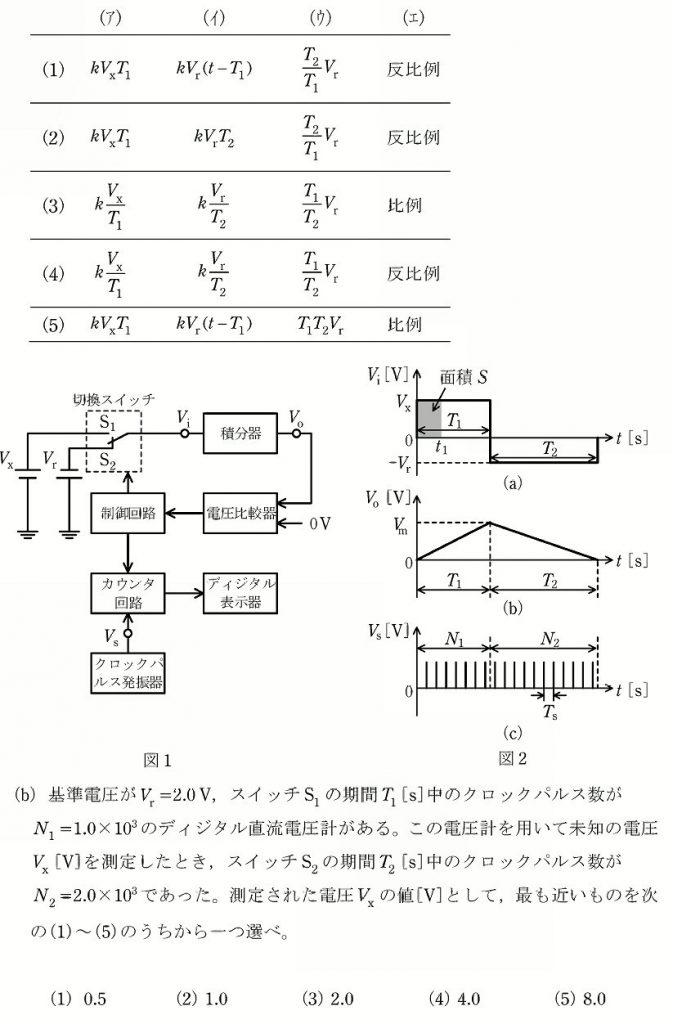
1…解説文と図より、kVxT1と容易に求まります。
2…時刻T1の段階でVmまで充電された電荷をkVr(t-T1)で放電していくことになります。解説文と図から容易に求まります。
3…動作原理より、入力電圧が高いほどT1におけるVmの値は大きくなるため、それを0Vまで放電していくのにかかる時間T2は長くなることになります。解説文より、T1は固定ですから、例えば入力電圧Vx=VrならT2=T1、Vx=2VrならT2=2T1…となることが読み取れます。したがって(T2/T1)Vrと分かります。
4…周期と周波数は反比例の関係です。
以上より、正解は(1)です。
(b)
(a)が求まればそれに当てはめて求めるだけです。基準電圧が2Vで、測定電圧で充電された電荷を放電するのに充電の2倍の時間がかかっていることは、測定電圧は2×2=4Vです。正解は(4)です。