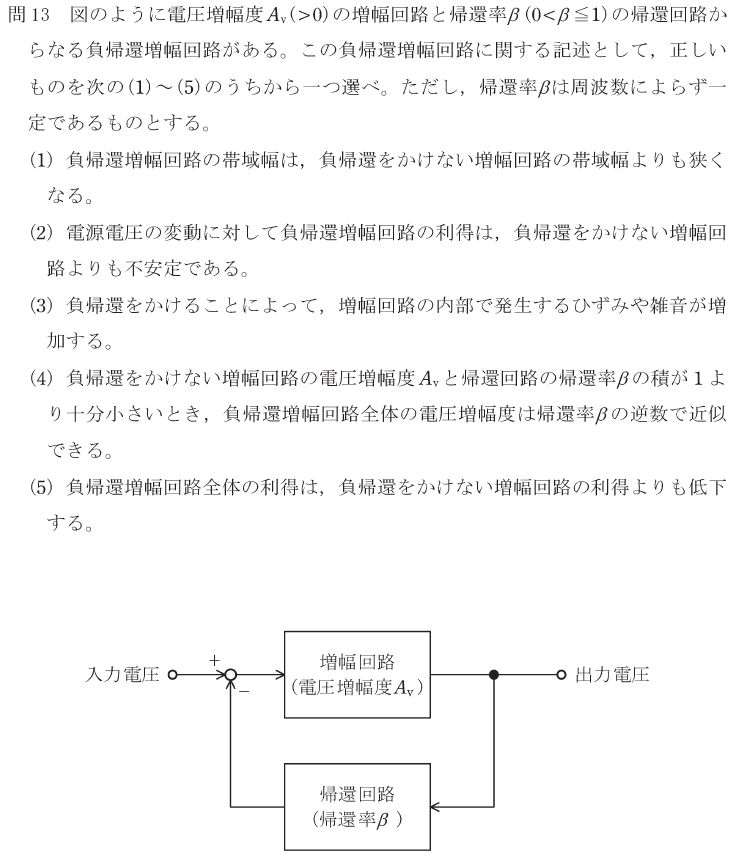
一般に増幅回路増幅度は、低い周波数と高い周波数で落ち込み、中間の周波数が最も増幅率が高いという山型の特性を持っています。負帰還を掛けることによって、この中間部分の増幅度の山を抑えて平らに均すという働きをします。したがって、負帰還率が高ければ高いほど見かけの増幅度は小さくなりますが、周波数特性は広い範囲にわたって均一となります。もちろん、電源電圧や周囲温度などの変動による増幅回路の特性変化も、負帰還率によって抑え込まれる利得以上の暴れであれば抑え込まれます。
以上より、(1)(2)(3)は誤りで、(4)については増幅回路の入力を1、出力をA、帰還回路の出口をβAとおくと、入力は1-βA、出力はAとなるので、回路全体での増幅度は
A/(1-βA）
です。このときβAが1より十分小さいときの回路利得はAとなるので、これも誤りです。
正解は（5）です。
高校物理の力学の基礎の問題です。
電界Eの中でqクーロンの点電荷が受けるクーロン力は
で求められます。このときの点電荷の加速度は、運動方程式より、
となります。点電荷はこの加速度を受けて右側に運動します。
初速度v0、加速度aの物体のt秒後の変位は、
ですから、これにv0=0、a=qE/m、そして点電荷の変位x=d/2を代入することでtが求まります。これを求めると、
となり、答えは(1)となります。
太陽電池は、ダイオードと同じPN接合の接合面に光を導入し、光のエネルギによって電子と正孔が生成され、それを外部に取り出すことで電池とするものです。したがって、（ア）はダイオード、（イ）は正孔です。
（ウ）の選択肢は、エネルギ保存の法則から導けます。太陽電池は、降り注いだ光エネルギの一部を電気エネルギに換えて取り出す装置ですから、もし電気エネルギを取り出さなければ、降り注いだエネルギは結局すべて太陽電池内で熱エネルギとなります。
したがって、負荷接続後の太陽電池温度は低くなることになります。正解は（1）です。
RC直列回路の時定数は、τ=RCで求められます。
時定数というのは、放射能の半減期のようなもので、どのくらいの早さで減少していくかという目安の値です。RC直列回路の場合、コンデンサCの静電容量が大きいほど大量の電荷が貯まっているので放電に時間がかかりますし、また抵抗Rの値が大きいほど流れる電流も小さくなるため、やはり放電に時間がかかります。これらを考えると、RCの積が時定数となることが分かります。なお、RL直列回路の場合は、コイルLの作用が大きいほど時間変化が緩やかになりますが、抵抗Rが大きいほどそもそも回路に流れる電流自体が小さいためコイルの作用が相対的に弱くなります。したがってRL直列回路の場合の時定数はτ＝L/Rとなります。
以上より、この回路の時定数を計算すると、
τ=100×10^-6×1×10^3=0.1
ですので、正解は（1）（2）（3）のどれかになります。
次に、十分時間が経過したときに抵抗で消費されるエネルギは、放電前にコンデンサに蓄えられていたエネルギになります。これは
W=CV^2/2
で計算できますので、これを求めると、
W=(1/2)×100×10^-6×1000×1000=50
となり、50Jと求まります。以上より正解は(2)です。
まず、各々の周波数におけるコンデンサとコイルのリアクタンスを求めます。コンデンサは1/jωC、コイルはjωLです。
以上より、ω2の場合に並列共振となり、回路電流は最小になることが分かります。この時点で正解は(3)か(4)です。
次にω1とω3の比較です。馬鹿正直にコイルとコンデンサの並列合成リアクタンスを計算し、電源電圧1Vを用いて実際に流れる回路電流を計算しても良いのですが、
LC並列部分に流れる電流は、LとCの電流が互いに逆位相であるため、各々の電流の差が合成電流となる
ことを念頭に置いて考えれば、すぐに正解が求まります。
なので、ω3の方が合成電流が大きくなることは即座に求まります。（どうしても実際に計算してみないと気が済まないのであれば、電源電圧を30Vにして計算してみると楽です。ω1の合成電流は4.5A、ω3の合成電流は9Aになります）
したがって正解は(3)です。
これは少し悩んだ問題ではないでしょうか。重ね合わせの原理を使う所までは求められても、そこから先悩んだかと思います。
電源が複数存在する線形回路ですから、重ね合わせの原理を使います。
まず交流100Vの電源を残して考えると、抵抗に流れる電流は10[A]、コンデンサに流れる電流は90度位相が進んだ+j10[A]です。この二つの合成電流は、1:1:√2の三角形より、10√2[A]と求まります。
次に直流電源だけを残した回路です。このとき定常状態ではコンデンサに電流が流れないので、回路電流は10[A]です。
以上の二つの電流（交流の10√2[A]と、直流の10[A]）の重ね合わせの実効値を求めるためには、実効値の定義「2乗の√」を用います。これを計算すると、
√{（10√2)^2 + 10^2 ) =√300=10√3≒17.32…[A]
従って答えは（3）です。
これもラッキー問題です。
直流電源をつないだ定常状態において、コンデンサには電流が流れません。また、コイルは単なる電線として振る舞います。したがって、この回路は、電源電圧Vと並列にR3とR2が接続されているだけの回路と等価です。
R2とR3の並列抵抗を求める式は、
1/R=1/R2 + 1/R3
より、
R=1/(1/R2 + 1/R3)
です。したがって、回路に流れる電流は、電源電圧Vをこの抵抗値で割ったものですから、答えは（4）です。
ラッキー問題です。
条件から、電流計と直列の10Ωに流れる電流は5Aなので、50ΩとRの並列部分には差し引き50Vの電圧が掛かっていることがすぐに分かります。
50Ωの両端に50Vの電圧が掛かれば、ここに流れる電流は1Aです。したがって、Rには4Aの電流が流れることになります。以上より、Rで消費される電力は、
50Vの電圧が掛かっていて4Aの電流が流れているときの電力
を求めればいいわけですから、50×4＝200Wです。正解は（5）です。
これはラッキー問題です。
回路全体を見ると、上側が60Ωと（20+20+20=）60Ωの並列、つまり30Ωです。これに下側の（10+4+6）＝20Ωが直列なので、回路全体としては100Vの電池に50Ωの抵抗が接続されているものとみなせます。したがって回路電流は2Aです。
さてここで、電池の＋極から20Ω-A点-20Ω-B点-20Ωと至る経路について考えます。上側は60Ωが2本の並列で30Ω、そこに2Aの電流が流れるので、20Ω-A点-20Ω-B点-20Ωの部分に流れる電流は1Aです。したがって、3本の20Ωは、それぞれ20Vずつの電圧降下です。
下側の4Ω・6Ω・10Ωは2Aの電流が流れます。したがって電圧降下は、それぞれ8V・12V・20Vです。以上のことから回路全体の電位を考えます。
電池のマイナス端子を基準にすると、
D点…8V
C点…8V+12V＝20V
下側の10Ωの右側端子…20V＋20V＝40V
B点…40V+20V=60V
A点…60V+20V＝80V
となりますから、
A-D間…80V-8V＝72V
B-C間…60V-20V=40V
となり、正解は（5）です。
電気回路に置き換えると、「電池に抵抗体をつないだら電流が流れました。抵抗体の抵抗率はいくらですか」程度の簡単な問題です。
まず、磁気回路における起磁力は、コイルの巻き数×コイルの電流です。したがって、8000×0.1＝800となります。単位はアンペアターン（電流×巻数）です。
次に、磁路の抵抗を求めます。これは電気回路における抵抗体の式
電気抵抗値＝抵抗率×（抵抗体の長さ÷断面積）
と全く同じです。ただし、電気回路では抵抗率（数値が大きいほど電気抵抗が大きい）を用いるのに対し、磁気回路では透磁率（数値が大きいほど時期を通しやすい＝磁気抵抗が小さい）を用いるので、
磁気抵抗値＝(1/透磁率）×（磁性体の長さ÷断面積）
で求めます。
電気回路における電流は、磁気回路では磁束です。ただし、この問題では磁束密度で与えられていますので、磁束密度×断面積で正味の磁束の値を計算します。（人口密度は単位面積当たりの人数の値なので、それに全体の面積を掛ければ全体の人口が求まるのと同じ理屈です）これを計算すると、磁束φは、
φ＝1.28×1×10^-4
となるので、あとはオームの法則を用いて、
800÷(1.28×1×10^-4)＝(1/μ)・(0.2/1×10^-4)
が成立することから、μの値を計算すると3.2×10^-4が求まります。答えは（5）です。