「電験3種」タグアーカイブ
電験3種過去問解説 2019年電力問4
質量欠損をm(単位:kg)とすると、得られるエネルギはE=mc^2(単位:ジュール)で求められます。したがって、
- 0.001×(0.09×0.01)×300000000×300000000 [J]
が核分裂によって得られるエネルギです。
一方、石炭の質量をM[kg]とすると、
- M×2.51×10000 [kJ]
が石炭の発熱量です。したがって、
- M×2.51×10000×1000=0.001×(0.09×0.01)×300000000×300000000
を解いてMを求めればよいので、
- M=0.001×(0.09×0.01)×300000000×300000000÷(2.51×10000×1000)=3226.8
したがって正解は(4)です。
電験3種過去問解説 2019年電力問3
電験3種過去問解説 2019年電力問2
正解…(1)
この手の問題は覚えておくしかない知識問題ですが、電験3種で出題される衝動水車はペルトン水車しかないと言っていいですから、「〇〇は衝動水車である」とあれば真っ先にペルトン水車を挙げるということでほぼ大丈夫だと思います。
反動水車は色々な種類があり、フランシス水車・カプラン水車のほかプロペラ水車などもありますが、構造と原理を図解で見て覚えるのがよいでしょう。もっとも、この問題は、圧力水頭(要するに落差によって作られた水圧)を水車に吹き付ける速度水頭(水道のホースの先端を手で潰して水の勢いを増すのと同じことです)に変換し、ペルトン水車に当てることで動力を生み出す…ということが分かっていれば選択肢は(1)だけに絞られます。
電験3種過去問解説 2019年電力問1
電験3種過去問解説 2019年理論問18
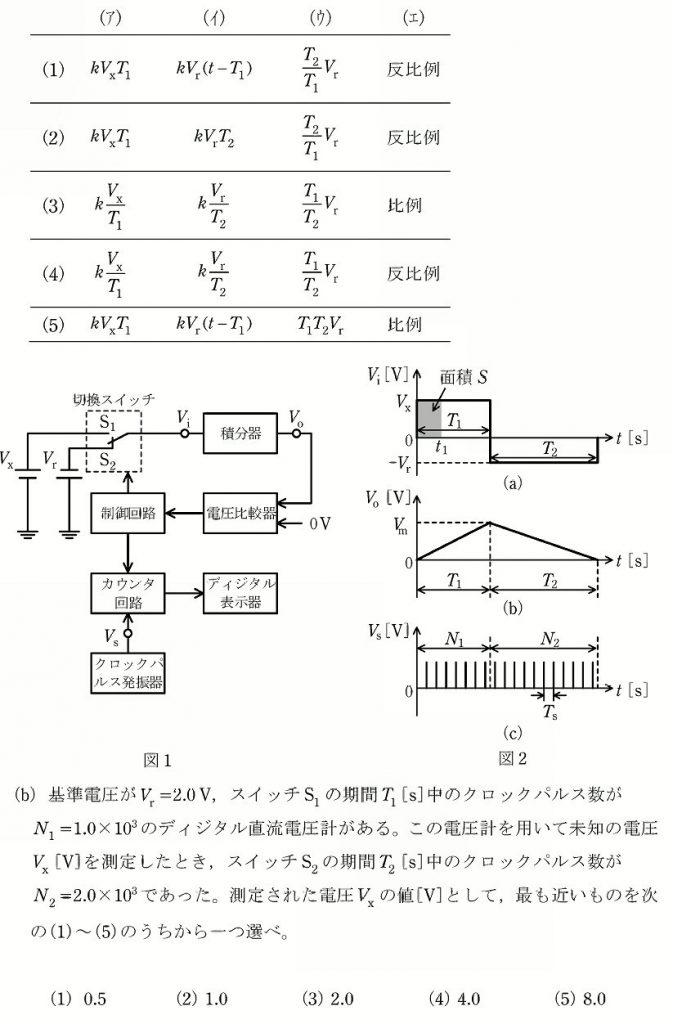
デジタルテスタ等で幅広く使われている二重積分型AD変換の基本原理に関する問題です。
(a)
1…解説文と図より、kVxT1と容易に求まります。
2…時刻T1の段階でVmまで充電された電荷をkVr(t-T1)で放電していくことになります。解説文と図から容易に求まります。
3…動作原理より、入力電圧が高いほどT1におけるVmの値は大きくなるため、それを0Vまで放電していくのにかかる時間T2は長くなることになります。解説文より、T1は固定ですから、例えば入力電圧Vx=VrならT2=T1、Vx=2VrならT2=2T1…となることが読み取れます。したがって(T2/T1)Vrと分かります。
4…周期と周波数は反比例の関係です。
以上より、正解は(1)です。
(b)
(a)が求まればそれに当てはめて求めるだけです。基準電圧が2Vで、測定電圧で充電された電荷を放電するのに充電の2倍の時間がかかっていることは、測定電圧は2×2=4Vです。正解は(4)です。
電験3種過去問解説 2019年理論問17
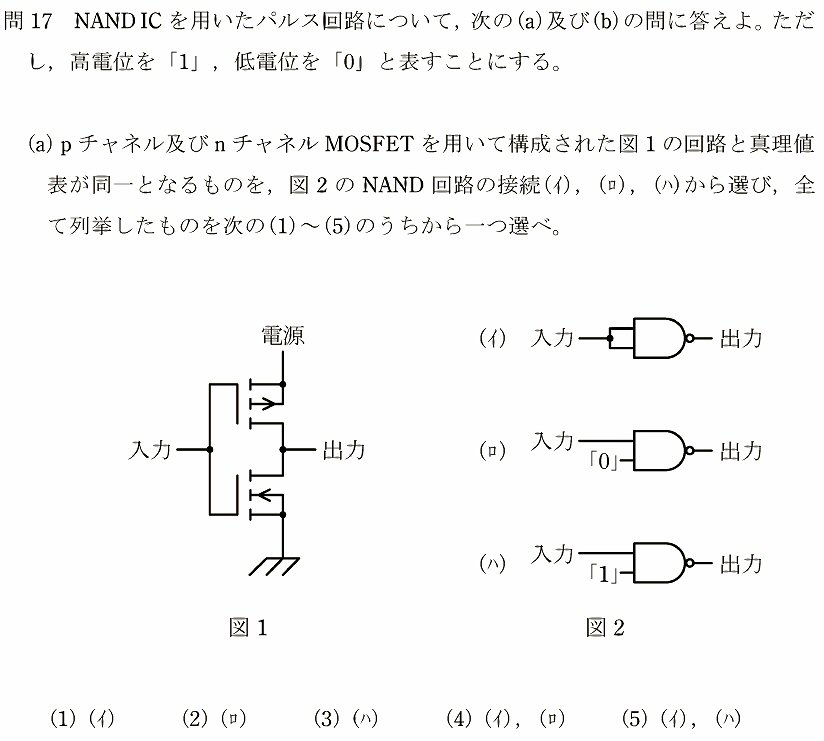
(a)
図1を見ると、上側がPchMOSFET、下側がNchMOSFETですから、入力が0のとき出力が1、入力が1のとき出力が0となるインバータとして動作します。
図2を見ると、NANDゲートは「11のとき出力が0、それ以外は出力が1」ですから、インバータとして動作するのはイとハです。正解は(5)です。
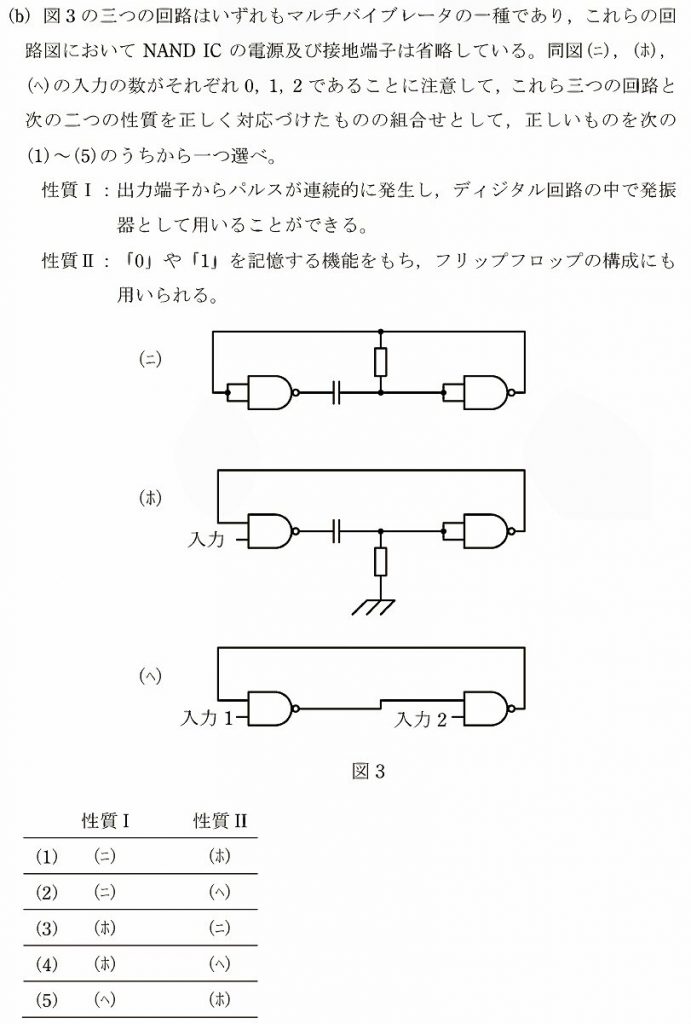
(b)
デジタル回路が苦手だと解析が難しい!と思うかもしれませんが、実はラッキー問題です。
性質Iを満たすには、入力端子が無くても自動的に動作し続ける(発振し続ける)必要がありますから、これは回路ニです。性質Ⅱを満たすには、入力が2つある必要がありますから、これは回路ヘです。したがって正解は((2)です。
電験3種過去問解説 2019年理論問16
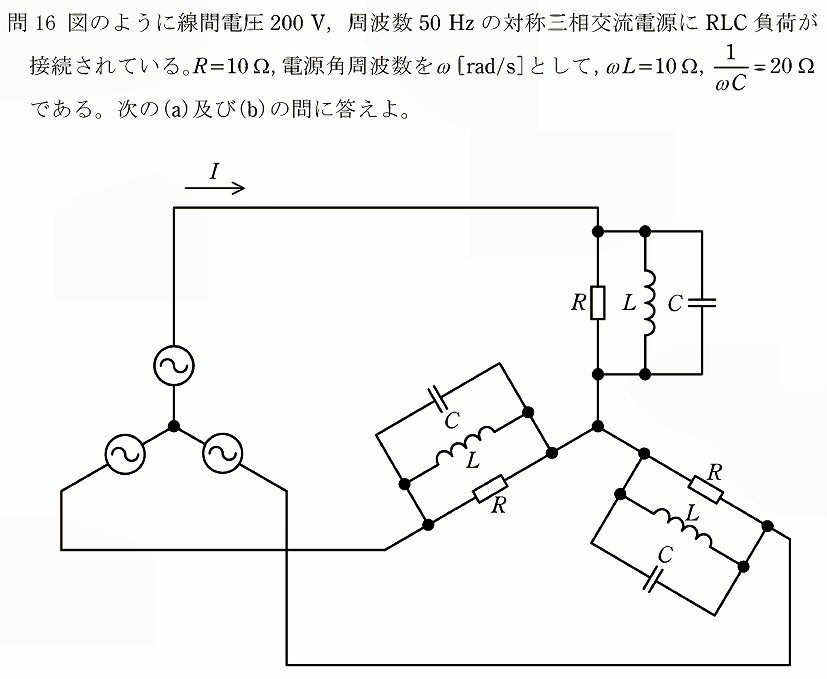
電源側がY結線、負荷側もY結線、そしてコイルやコンデンサのリアクタンス値も既に書かれているので、ラッキー問題です。一問前が少し難しかったので調整したかな?但し、電圧が線間電圧で与えられているため、相電圧は√3で割った115Vで考える点にだけ注意が必要です。
(a)
負荷一相当たりで考えます。LCの並列サセプタンスは|1/10-1/20|=1/20[S]なので、リアクタンスは20Ω、したがってLC並列部分に流れる電流は5.77Aです。抵抗に流れる電流は115÷10=11.5Aですから、5.77Aと10Aの二乗平均を取ると約13Aとなり、答えは(3)です。
(b)
第2種電気工事士レベルの超ラッキー問題です。電力を消費するのは抵抗だけですから、一相当たり115V×11.5A≒1.33kW、これが3本で合計約4kWです。正解は(4)です。
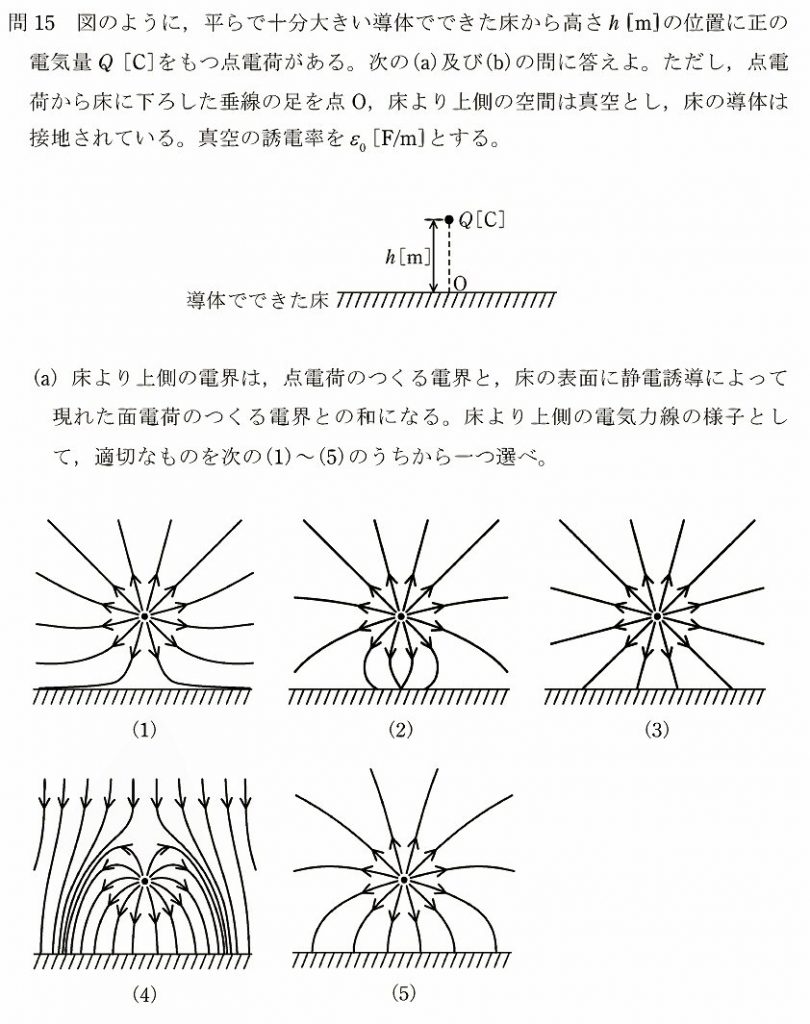
電験3種過去問解説 2019年理論問15
(a)
電気力線は、電界の様子を可視化した線です。電気力線と電界面とは垂直に交わるので、導体床面(=電位がゼロ)に対しては垂直に入らなければいけないはずです。これに合致するのは(5)です。
(b)
本来は、力学の仕事の定義を理解していないと解けない問題です。仕事は(力)×(距離)で求めますので、クーロン力と移動距離の積で求めます。題意より、点Oに固定した電気量ーQ/4のクーロン力からhの距離にあるQの電荷が受ける力は、クーロンの法則より
F=Q^2/(16πε0h^2)
ですから、求める仕事は∫Fdxとなり、xをhからzまで積分したものとして求められます。これを計算すると(3)の式が求まります。
しかし、これは積分の知識が必要ですから、電位の定義と電位を求める公式から解いてくださいということだと思います。Qクーロンから距離rの点の電位は、
V=Q/4πε0r
で求められますが、電位とは「単位電化を無限遠からその位置まで持ってくるのに必要な仕事」を意味しますから、この式を用いてQ/4クーロンからhの点とzの点での電位差を求め、その値にQを掛けた値として解答を導き出してくださいという問題です。
いずれにしても答えは(3)となります。