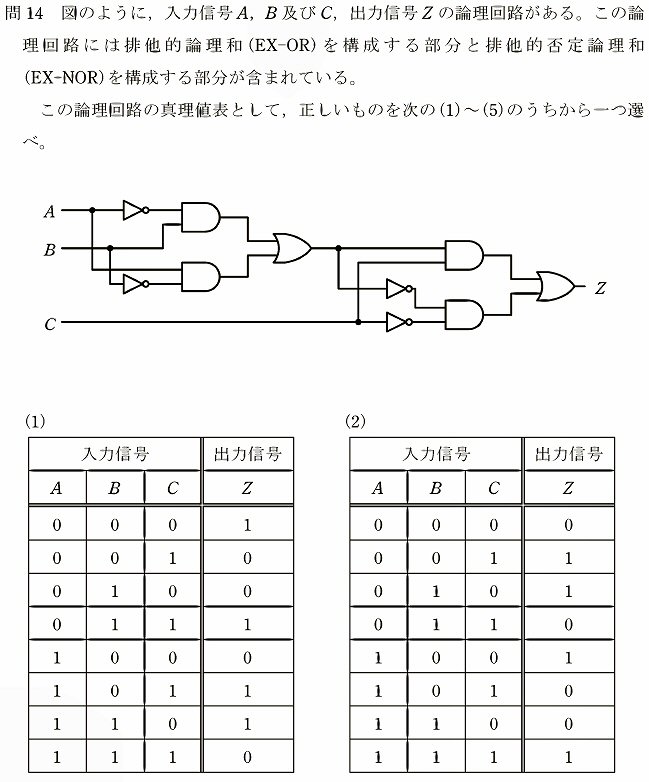
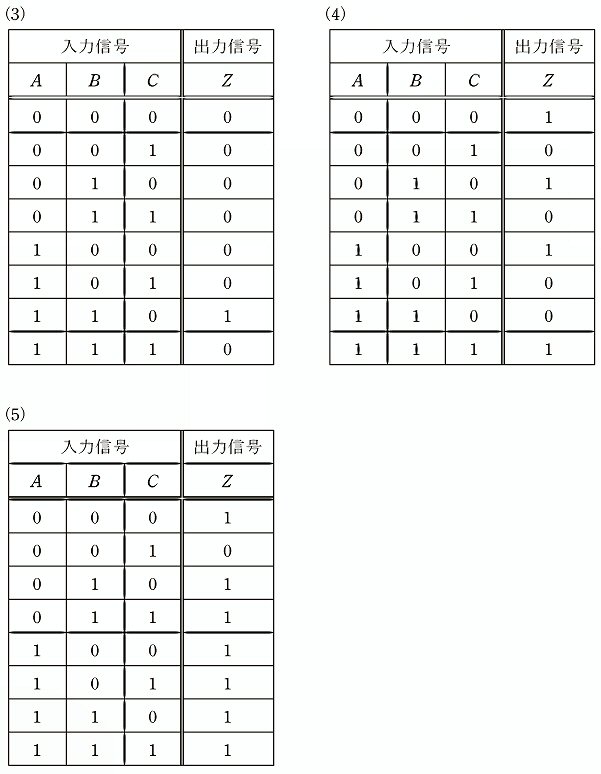
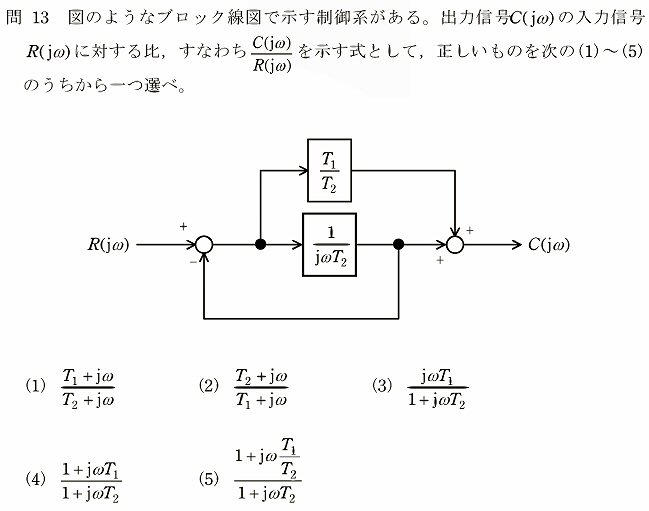
(a)
変圧器は、電圧が巻数比、電流は巻数の逆数の比、そして抵抗・リアクタンス・インピーダンスは巻数比の2乗で変換します。(理論の基礎です)
したがって、まずは二次側の抵抗・リアクタンスを一次側に変換します。6600V:200Vということは33:1ですから、二次側の値を33^2して、
この2値の二乗の√を取ると約6.3706…となるので、答えは(4)です。
(b)
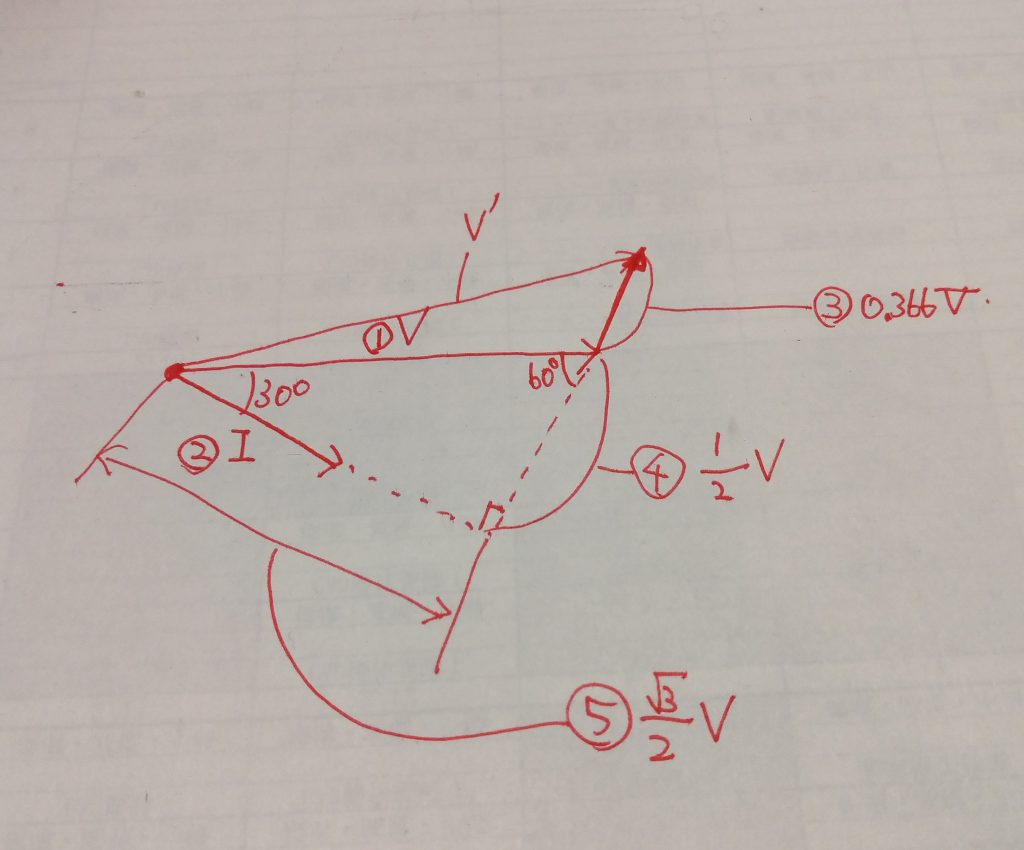
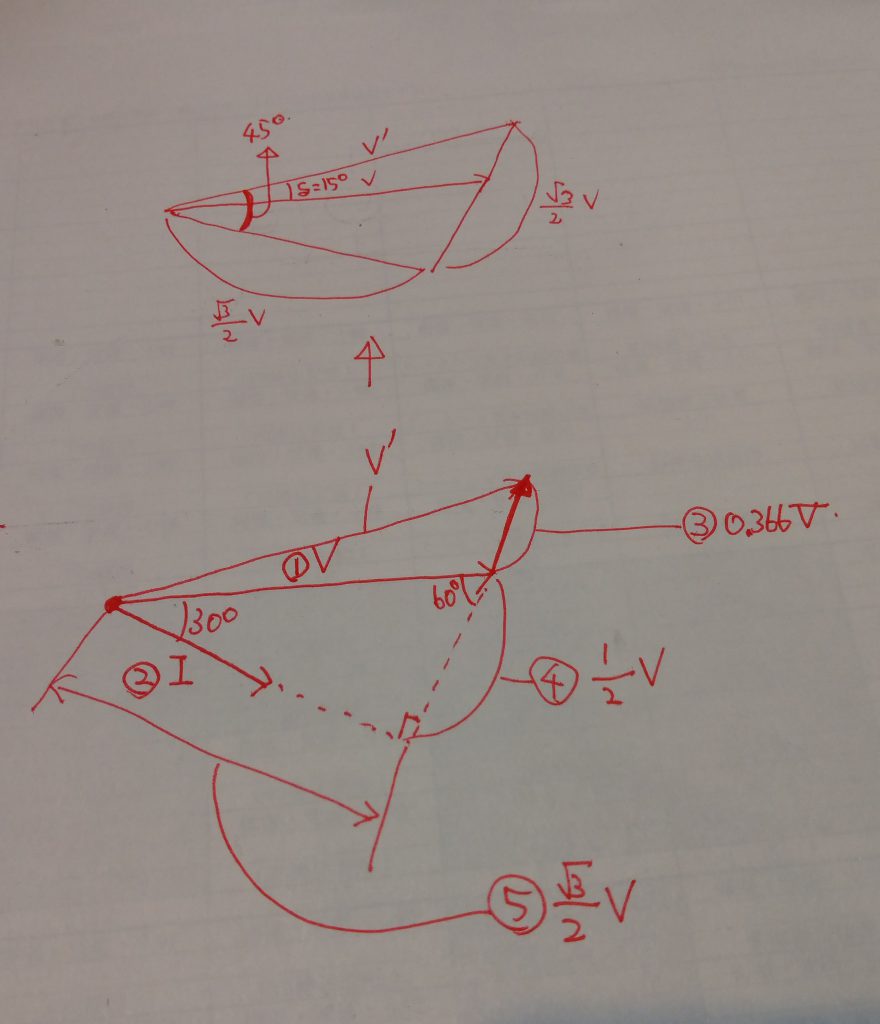
前問で一次側に変換した直列インピーダンスを使い、「二次側200V、200kVA、力率遅れ0.8」を「二次側6600V、200kVA、力率遅れ0.8」として計算すれば求まります。
6600Vで200kVAの負荷に流れる電流は30.3Aです。
したがって、V=I(rcosθ+xsinθ)の式より、
V=30.3×(1.1445×0.8+6.267×0.6)≒141.67…
従って、一次電圧は6600+141.67≒6740Vとなり、答えは(3)となります。
出題文にヒントが書いてあるので簡単です。左側の一段目と右側の二段目では、左側がXOR、右側がXNORです。慣れれば真理値表を書かなくても見ただけで分かりますが、そうでなくても右側の部分に(1,1)を入力してみると、上側のANDの出力は1、その出力をORに入れたのが出力ZですからこれはXNORと分かります。
したがって、出力が1となる条件は、
と求まります。これに合致するのは(1)です。
「どこかを１と置き、そこから辻褄を合わせる」ことで答えが求まります。ここでは、T1/T2と1/(jωT2)の入力部分を１とします。これを基にして各部の値を求めると、入力は１＋1/(jωT2)、出力はT1/T2+1/(jωT2)となります。これよりC/Rを求めると、(1+jωT1)/(1+jωT2)と求まり、答えは(4)です。
リチウムイオン電池の正極はリチウムを含む金属酸化物、負極に黒鉛を用います。電解液は有機電解液で、この中をイオンが移動することで電池として振る舞います。放電時、リチウムイオン（プラスイオン）が負極から正極に移動し、正極で外部回路を流れてきた電子と結合します。セル当たりの電圧は3.7～3.8Ｖ程度です。したがって、答えは(1)です。
直流電源からスイッチングによって交流を作り出す装置はインバータと言います。
電力変換器のスイッチングデバイスは、当然ながらオン・オフ制御を行います。オン制御だけしか出来なければ電源が短絡されてしまいます。
バルブデバイスには、逆向きにダイオードを接続し、交流負荷のリアクタンス分に起因する逆電圧を還流させます。
交流電圧を変化させるためには、直流電圧源の電圧を変えることで交流側の波高値を変化させるか、あるいはスイッチングパルス幅を変化させるかという手段があります。この制御はPWM（Pulse Width Modulation）と呼びます。
以上より、答えは（5）です。
毎分300㎥、全揚程10mということは、一秒あたりに必要なエネルギは位置エネルギmghより、
ポンプ効率が80％という事から、必要な電力は、
従って、6台では若干不足し、7台必要となります。正解は（4）です。
単巻変圧器は、（一次電圧と二次電圧の差）×（二次電流）の電力を供給します。
消費電力200kW、二次電圧6600V、力率0.8という条件から、二次電流は
と求まります。また、一次電圧と二次電圧の差は600Vですから、自己容量は、
となり、答えは（1）です。メチャクチャ簡単なラッキー問題です。
a
誘導電動機は、固定巻線による回転磁界の中に、無給電で両端を低抵抗で短絡した回転コイルを配置したものです。回転コイルは、外部から与えられた回転磁界によって電圧が誘起され、電流が流れます。これは変圧器の一次巻線と二次巻線の関係と同じです。二次側の負荷抵抗値が滑りsによって見かけ上変化するのは誘導電動機ですから、（ア）は誘導電動機、（イ）は変圧器です。
b・c
電動機は回転コイルと固定コイルの間に発生する電磁力を取り出す装置ですが、これらをどちらも外部から制御できるのは直流電動機や同期電動機です。（誘導電動機は回転コイルに誘起される電圧を制御しにくい）
ここで、（エ）の出力に負荷角が関与するという記述より、（エ）は同期電動機、（ウ）は直流電動機と決定できます。以上より、答えは（3）です。
ステッピングモーターは、与えられたパルスによって一定角度ずつ回転する構造になっています。これにより、パルス数で回転角度を制御でき、パルス周波数で回転速度を制御することができます。以上より、（ア）はパルス数、（イ）は回転角度、（ウ）は周波数です。ここまでの選択肢で正解は（5）と決定されます。
（エ）はステップ角。（オ）は、回転子の永久磁石による磁力が働くため、無通電状態でも外部からの回転トルクに対して保持力が働きます。
まず、発電機の出力端子の電圧を横向きの基準ベクトル①として描きます。次に、負荷力率が遅れcos30°という条件から、①のベクトルから遅れ側に負荷電流Iのベクトル②を描きます。ここまでがまず第一段階です。
次に、「電機子電流が定格電流の40％」「同期リアクタンスが0.915p.u.」という条件から、同期リアクタンス（電気子巻線と出力端子の間に直列に入っているリアクタンス）の両端に発生している電圧を求めます。
百分率同期リアクタンスというのは、発電機が定格電圧・定格電流で運転している時の負荷のΩ値に対して、同期リアクタンスのΩ値が何％であるかを表しています。従って、定格負荷のとき、同期リアクタンスの両端に発生している電圧は定格出力電圧の91.5％であることが分かります。ここで、「電機子電流が定格電流の40％」という条件より、同期リアクタンスの両端に発生している電圧は定格運転時の40％の値であることが分かります。これを計算すると、0.915×0.4＝0.366p.u.ですから、同期リアクタンスの両端に発生している電圧は出力電圧Vの0.366倍と求まり、これを③として描きます。同期リアクタンスの両端に発生する電圧は、流れる電流に対して進み90°となるため、図のようなベクトルになります。
ところで、30°・60°・90°の直角三角形の性質から、④の長さがV/2、⑤の長さが√3V/2であることが求まります。ここで③と④の長さを足すと0.866V＝√3V/2ですから、電機子に発生している電圧V’は⑤と（④＋③）とV’の直角三角形の関係となり、これは1：1：√2の45°の三角形と求まります。従って、相差角δは15°と求まります。
