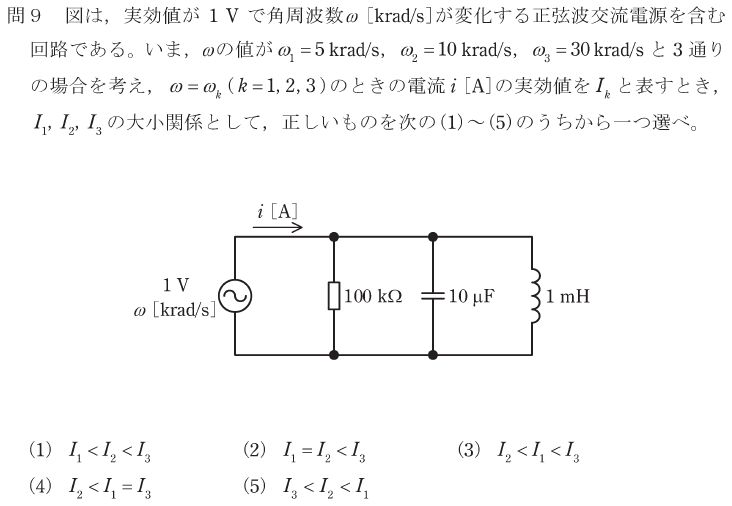
まず、各々の周波数におけるコンデンサとコイルのリアクタンスを求めます。コンデンサは1/jωC、コイルはjωLです。

• ω1…コンデンサ-j20[Ω]、コイル+j5[Ω]
• ω2…コンデンサ-j10[Ω]、コイル+j10[Ω]
• ω3…コンデンサ-j3[Ω]、コイル+j30[Ω]

以上より、ω2の場合に並列共振となり、回路電流は最小になることが分かります。この時点で正解は(3)か(4)です。

次にω1とω3の比較です。馬鹿正直にコイルとコンデンサの並列合成リアクタンスを計算し、電源電圧1Vを用いて実際に流れる回路電流を計算しても良いのですが、

LC並列部分に流れる電流は、LとCの電流が互いに逆位相であるため、各々の電流の差が合成電流となる

ことを念頭に置いて考えれば、すぐに正解が求まります。

• ω1…リアクタンス5Ωのコイルに流れる電流から、リアクタンス20Ωのコンデンサに流れる電流を引いたものが合成電流
• ω3…リアクタンス3Ωのコンデンサに流れる電流から、リアクタンス30Ωのコイルに流れる電流を引いたものが合成電流

なので、ω3の方が合成電流が大きくなることは即座に求まります。（どうしても実際に計算してみないと気が済まないのであれば、電源電圧を30Vにして計算してみると楽です。ω1の合成電流は4.5A、ω3の合成電流は9Aになります）

したがって正解は(3)です。