CファラドのコンデンサにQクーロンの電荷が貯まっているとき、極板間電圧は

V=Q/C

で求まります。また、極板面積S、極板間距離d、誘電率εのコンデンサの静電容量は、

C=εS/d

で求まります。

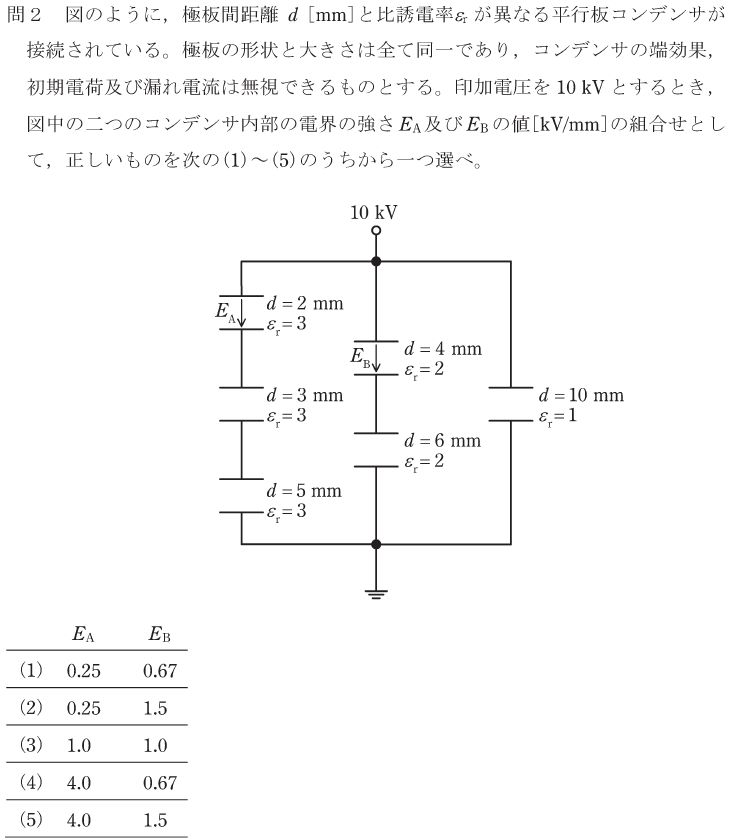
ここで回路を見ると、左の3直列のコンデンサは、極板の形状と大きさは全て同一であることから、静電容量の比は上から順に

3/2：3/3：3/5

となります。一方、V=Q/Cの式より、直列コンデンサ（＝流れた電荷量は全て同じ）の極板間電圧は静電容量Cの逆数の比になることが分かりますから、左の3直列のコンデンサの電圧比は、上から順に

2/3：3/3：5/3

となります。ここで電圧比を整数に直すと、分母が全て3なので

2:3:5

と分かります。これらの合計が10kVですから、コンデンサの極板間電圧は上から順に

2kV：3kV：5kV

です。

電界の強さは、二点間の電圧差をその距離で割った値なので、EAの大きさは、

2kV÷2mm＝1kV/mm

となり、この時点で正解は(3)しかありません。

EBの求め方も同じです。真ん中の2直列のコンデンサの静電容量比は、

2/4：2/6

ですから、電圧はこの逆比の

4/2：6/2＝4：6

です。したがって真ん中上側コンデンサの極板間電圧は4kVです。

これより、EBの値は

4kV÷4mm＝1kV/mm

となります。