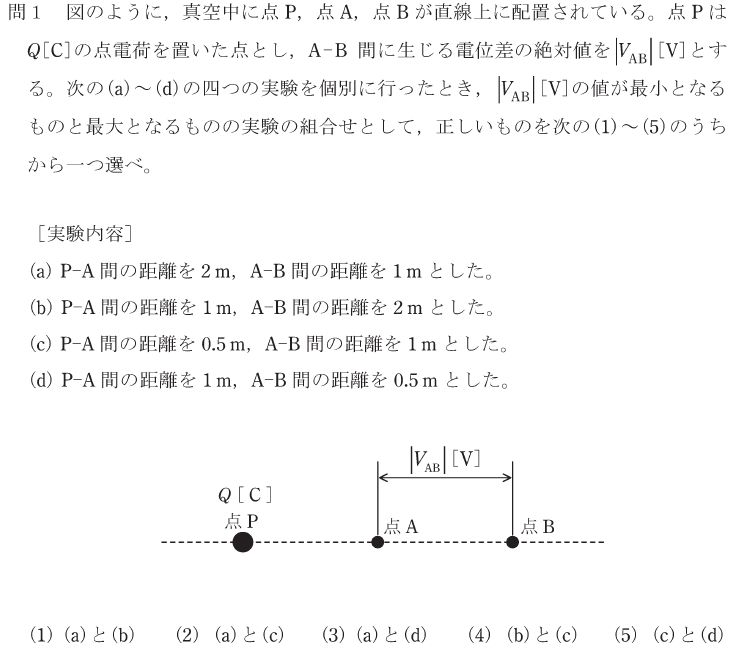
電位を計算する問題です。
点電荷Q[C]があるとき、そこから距離r離れた点における電位の絶対値は、誘電率をεとして
Q/4πrε
で求められます。これは、1Cの単位電荷に発生するクーロン力とその単位電荷を無限遠(r=∞)から距離rの点まで持ってくる仕事(クーロン力×距離)で定義されますが、この計算には積分が必要なため、電験3種の場合は単に式を覚えておけばOKです。
これに則って各々の電位差を求めていきます。(差を比べやすいよう、分母を6にして通分した値にしました)
(a)VAB=(Q/4πr)・|1/2-1/3|=(Q/4πr)・1/6
(b)VAB=(Q/4πr)・|1/1-1/3|=(Q/4πr)・4/6
(c)VAB=(Q/4πr)・|1/0.5-1/1.5|=(Q/4πr)・8/6
(d)VAB=(Q/4πr)・|1/1-1/1.5|=(Q/4πr)・2/6
以上より、電位差が最小のものは(a)、最大のものは(c)と求まります。正解は(2)です。