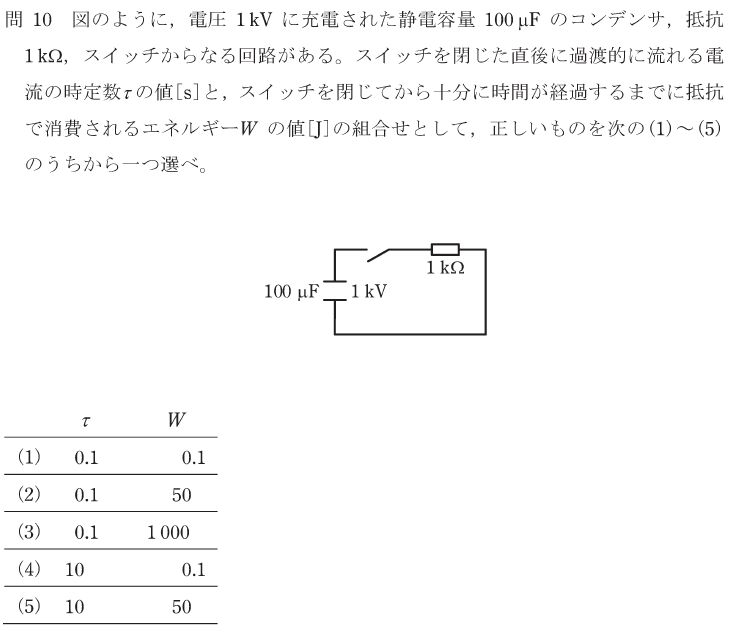
RC直列回路の時定数は、τ=RCで求められます。

時定数というのは、放射能の半減期のようなもので、どのくらいの早さで減少していくかという目安の値です。RC直列回路の場合、コンデンサCの静電容量が大きいほど大量の電荷が貯まっているので放電に時間がかかりますし、また抵抗Rの値が大きいほど流れる電流も小さくなるため、やはり放電に時間がかかります。これらを考えると、RCの積が時定数となることが分かります。なお、RL直列回路の場合は、コイルLの作用が大きいほど時間変化が緩やかになりますが、抵抗Rが大きいほどそもそも回路に流れる電流自体が小さいためコイルの作用が相対的に弱くなります。したがってRL直列回路の場合の時定数はτ＝L/Rとなります。

以上より、この回路の時定数を計算すると、

τ=100×10^-6×1×10^3=0.1

ですので、正解は（1）（2）（3）のどれかになります。

次に、十分時間が経過したときに抵抗で消費されるエネルギは、放電前にコンデンサに蓄えられていたエネルギになります。これは

W=CV^2/2

で計算できますので、これを求めると、

W=(1/2)×100×10^-6×1000×1000=50

となり、50Jと求まります。以上より正解は(2)です。