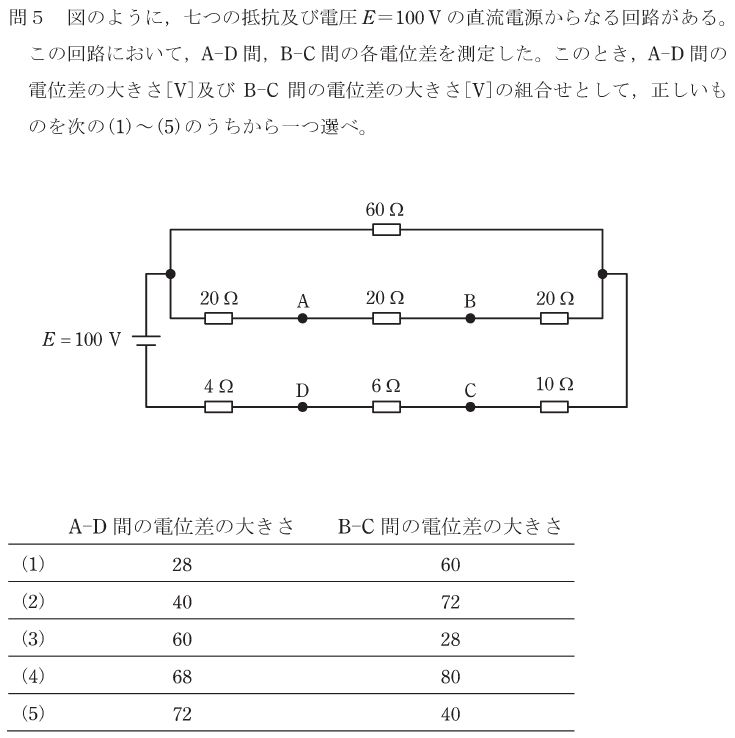
これはラッキー問題です。
回路全体を見ると、上側が60Ωと(20+20+20=)60Ωの並列、つまり30Ωです。これに下側の(10+4+6)=20Ωが直列なので、回路全体としては100Vの電池に50Ωの抵抗が接続されているものとみなせます。したがって回路電流は2Aです。
さてここで、電池の+極から20Ω-A点-20Ω-B点-20Ωと至る経路について考えます。上側は60Ωが2本の並列で30Ω、そこに2Aの電流が流れるので、20Ω-A点-20Ω-B点-20Ωの部分に流れる電流は1Aです。したがって、3本の20Ωは、それぞれ20Vずつの電圧降下です。
下側の4Ω・6Ω・10Ωは2Aの電流が流れます。したがって電圧降下は、それぞれ8V・12V・20Vです。以上のことから回路全体の電位を考えます。
電池のマイナス端子を基準にすると、
D点…8V
C点…8V+12V=20V
下側の10Ωの右側端子…20V+20V=40V
B点…40V+20V=60V
A点…60V+20V=80V
となりますから、
A-D間…80V-8V=72V
B-C間…60V-20V=40V
となり、正解は(5)です。