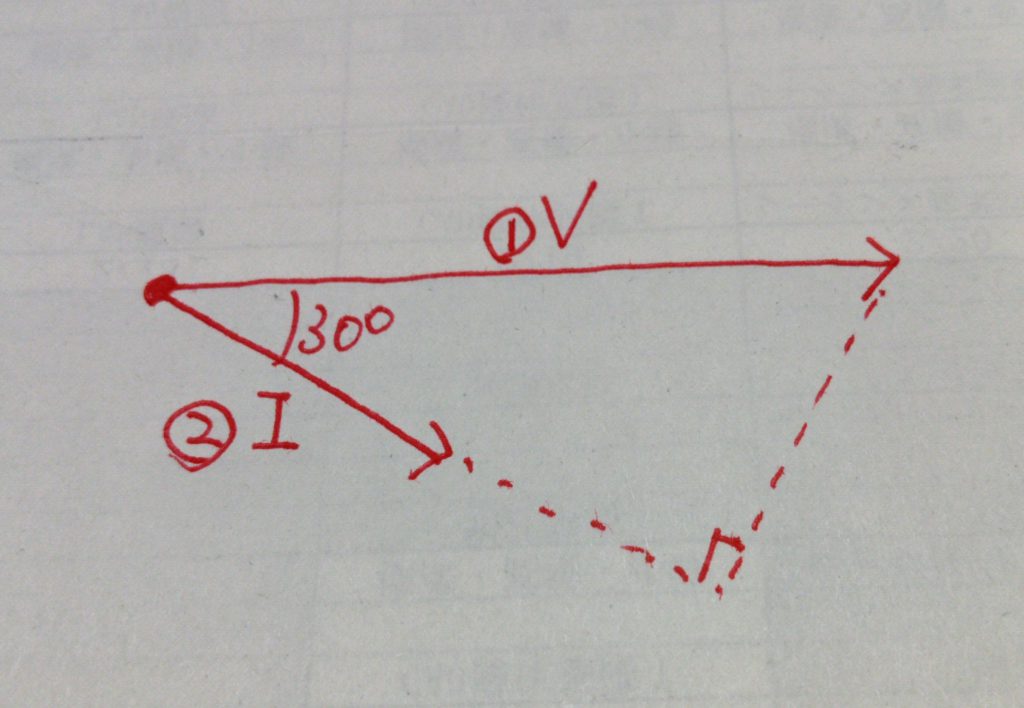
まず、発電機の出力端子の電圧を横向きの基準ベクトル①として描きます。次に、負荷力率が遅れcos30°という条件から、①のベクトルから遅れ側に負荷電流Iのベクトル②を描きます。ここまでがまず第一段階です。
次に、「電機子電流が定格電流の40%」「同期リアクタンスが0.915p.u.」という条件から、同期リアクタンス(電気子巻線と出力端子の間に直列に入っているリアクタンス)の両端に発生している電圧を求めます。
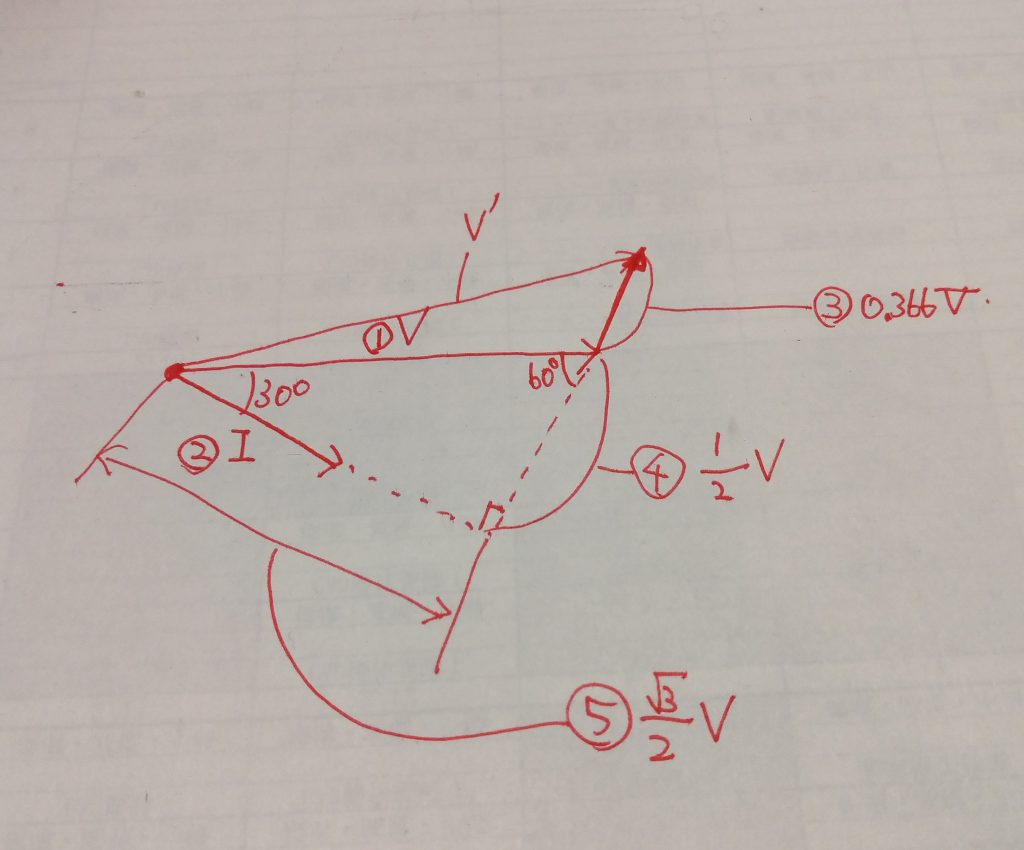
百分率同期リアクタンスというのは、発電機が定格電圧・定格電流で運転している時の負荷のΩ値に対して、同期リアクタンスのΩ値が何%であるかを表しています。従って、定格負荷のとき、同期リアクタンスの両端に発生している電圧は定格出力電圧の91.5%であることが分かります。ここで、「電機子電流が定格電流の40%」という条件より、同期リアクタンスの両端に発生している電圧は定格運転時の40%の値であることが分かります。これを計算すると、0.915×0.4=0.366p.u.ですから、同期リアクタンスの両端に発生している電圧は出力電圧Vの0.366倍と求まり、これを③として描きます。同期リアクタンスの両端に発生する電圧は、流れる電流に対して進み90°となるため、図のようなベクトルになります。
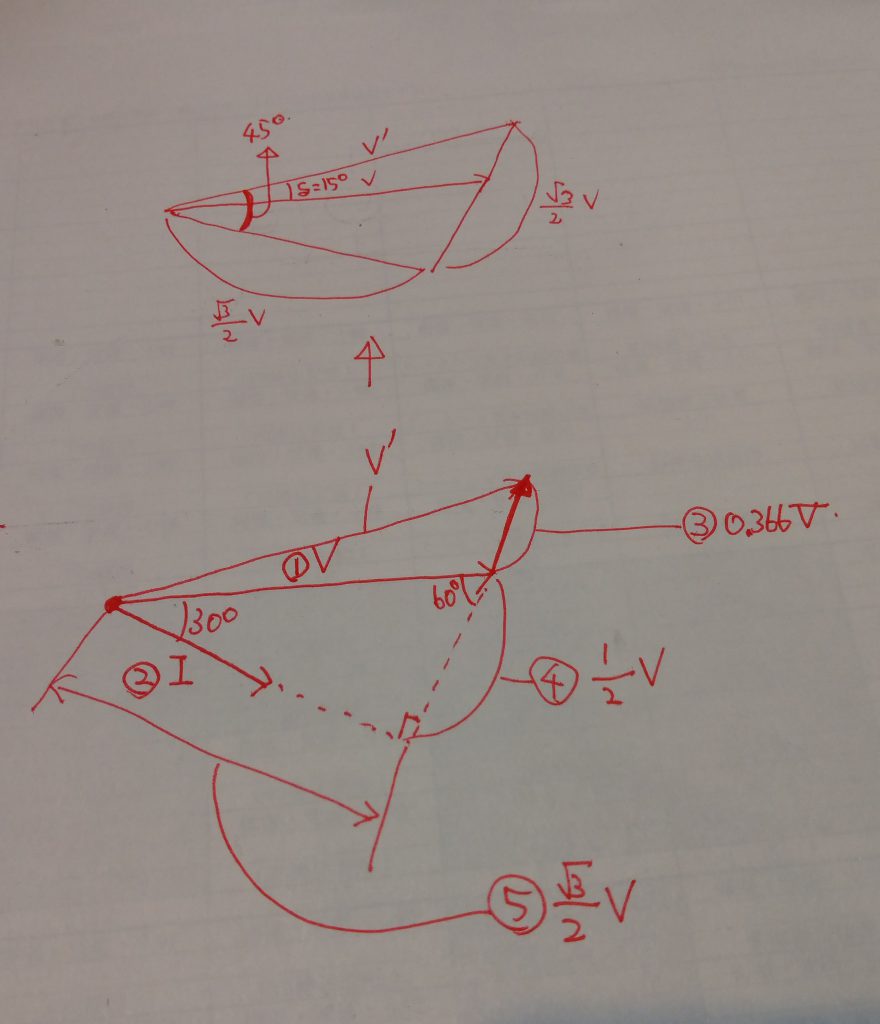
ところで、30°・60°・90°の直角三角形の性質から、④の長さがV/2、⑤の長さが√3V/2であることが求まります。ここで③と④の長さを足すと0.866V=√3V/2ですから、電機子に発生している電圧V’は⑤と(④+③)とV’の直角三角形の関係となり、これは1:1:√2の45°の三角形と求まります。従って、相差角δは15°と求まります。